It is well known that all of the fundamental constants of physics are finely tuned to make life possible in our universe; for example, see this nice video featured recently at ENV. It is also well known that many scientists, in order to avoid drawing the obvious conclusion from this fine-tuning, postulate the existence of a huge number of other unobservable universes, in which these constants have random values, so that one was bound to get lucky and produce numbers favorable to life.

What is not so widely noticed is that not only are the values of the constants of chemistry (the masses and charges of electrons, protons and neutrons, the strengths of the nuclear and electromagnetic forces, etc.) critical for life to exist in our universe, but the fundamental equation of chemistry, the Schroedinger equation, is itself critical for life.

We should not only wonder why Planck’s constant, which appears in the Schroedinger equation, has such a lucky value, but why are the motions of all particles governed by this partial differential equation? One of the most surprising things about our universe is the beautiful way in which mathematical equations can be used to elegantly model physical processes. In the case of macroscopic processes, such as diffusion or fluid flow, we can derive the equations from more basic processes, so that in these cases we feel we “understand” why the mathematics fits the physics.

But when we get down to the most fundamental particles and forces, we find they still obey an elegant mathematical equation, and we have absolutely no idea why — they just do. There is no conceivable reason why the effect that the fundamental forces have on the fundamental particles should be given by the (complex-valued!!) solution to a wave or eigenvalue partial differential equation (PDE), except that it results in elements and chemical compounds with extremely rich and useful chemical properties, and gives PDE software developers like me some very interesting applications to solve.

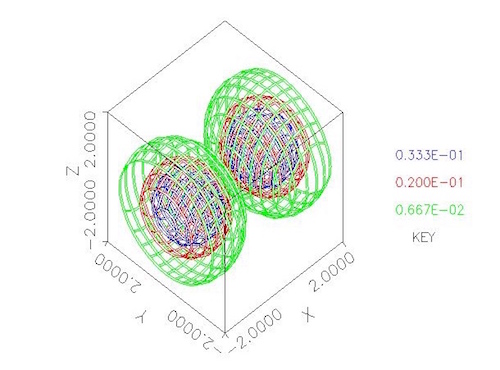
For example, the figure at the top of this post is a contour surface plot of the probability distribution for one energy state of an electron orbiting two protons, from Fitzgerald and Sewell 2000, which was obtained by solving the Schroedinger equation using my PDE solver, PDE2D. See the PDE2D web page for a list of over 225 journal publications in which the numerical results were produced by PDE2D, and a link to the new third edition of my PDE book (Sewell 2015).

If the elementary particles interacted by bouncing off each other like tiny balls obeying classical Newtonian laws, chemistry would be dead. In Partial Differential Equations (Strauss 2008), Walter Strauss writes:

Schroedinger’s equation is most easily regarded simply as an axiom that leads to the correct physical conclusions, rather than as an equation that can be derived from simpler principles…. In principle, elaborations of it explain the structure of all atoms and molecules and so all of chemistry!

Are we to assume that in all these other universes there are still electromagnetic and nuclear forces, electrons, protons, and neutrons, and the behavior of the particles is still governed by the Schroedinger equation; but the forces, masses and charges, and Planck’s constant, have different values, generated by some cosmic random number generator? Or perhaps the behavior of particles is governed by random types of partial differential equations in different universes, but there are still many universes in which Schroedinger’s equation holds, with random values for Planck’s constant?

No doubt there were some universes which couldn’t produce life because their fundamental equation of chemistry looked just like the Schroedinger equation, but with first derivatives in space where there should be second derivatives, or a second derivative in time where there should be a first derivative, or the complex number i was missing, or the linear Vu term was replaced by a nonlinear term Vu².

Any of the changes listed — and others not listed — would fundamentally alter the nature of the solutions, and chemistry as we know it would not exist. The fundamental equation of chemistry appears to itself be fine-tuned.

References:

Fitzgerald, Rosa and Granville Sewell (2000), “Solving Problems in Computational Physics Using a General-Purpose PDE Solver,” Computer Physics Communications 124, 132-138.

Sewell, Granville (2015), The Numerical Solution of Ordinary and Partial Differential Equations, 3rd edition, World Scientific Publishing Company.

Strauss, Walter (2008) Partial Differential Equations, an Introduction, second edition, John Wiley & Sons.